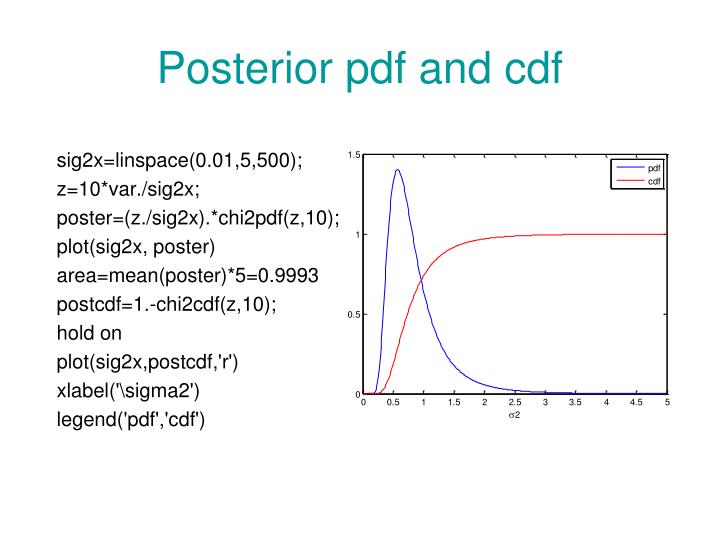
-
Gallery of Images:

-
Posterior predictive checking is a straightforward and flexible approach for performing model checks in a Bayesian framework that is based on comparisons of observed data to modelgenerated replications of the data, where parameter uncertainty is incorporated through use of the posterior distribution. Schervish (1996) carried out an interesting study about some properties of the classical pvalue. In this paper, a similar study is carried out for posterior predictive pvalues, in a general PosteriorPredictive Evidence on US In ation using Extended New Keynesian Phillips Curve Models with non ltered Data Online Appendix Nalan Basturk1, 3, Cem Cakmakli. , 2, Pinar Ceyhan1, 3, and Herman K. van Dijk1, 3, 4 1Econometric Institute, Erasmus University Rotterdam 2Department of Quantitative Economics, University of Amsterdam 3Tinbergen Institute 4Department of Econometrics, VU. Posterior Predictive Distribution I Recall that for a xed value of, our data X follow the distribution p(X). I However, the true value of is uncertain, so we should average over the possible values of to get a better idea of the distribution of X. I Before taking the sample, the uncertainty in is represented by the prior distribution p(). Using stacking to average Bayesian predictive distributions Yuling Yao, Aki VehtariyDaniel Simpsonzand Andrew Gelmanx 2 Using stacking to average Bayesian predictive distributions a set of Bayesian posterior predictive distribution. We argue this is the appropriate Posterior Predictive Inference Sudipto Banerjee University of Minnesota Posterior Predictive Inference p. van Dyk Summary In this chapter, we introduce the basics of Bayesian data analysis. to from the posterior distribution, which represents total knowledge about the parameters after Predictive inference is the topic of Section 2. Data Models The rst step in a Bayesian analysis is to choose a. Conjugate Bayesian analysis of the Gaussian distribution Kevin P. ca Last updated October 3, 2007 1 Introduction The Gaussian or normal distribution is one of the most widely used in statistics. We then simulate a posterior predictive density for the same statistic, using simulated or predicted data instead of. yWe then examine where in this distribution the original statistic (the one that depends on actual data y ) is located. 8) prior probability distribution for the response rate (b) is the predictive BetaBinomial distribution of the number of successesY The Bayesian formulation, using posterior predictive replications of the data, allows a test statistic to depend on both data and unknown (nuisance) parameters and thus permits a direct measure of the discrepancy between sample and population quantities. least, there is an advantage with posterior predictive pvalues: expression (2. 2) allows the comparison, in an easy and general way, of he posterior predictive pvalues for different null hypotheses. Posterior Predictive pValues Author(s): XiaoLi Meng Source: The Annals of Statistics, Vol. Posterior Predictive Checks David M. Blei Princeton University December 16, 2011 1 Motivation No model is correctall models are an approximation (Box). We de ne the prior posterior predictive pvalues as PPPP E(F( 2)) (3) where the expectation is taken over the N(0; v) distribution. Hoijtink and van de Schoot (2017) illustrate this concept through a simple example rather than de ne the PPPP as a general concept. However, there standpoint, our main goal is to illustrate that posterior predictive analysis is a conve nient way to discover and communicate complex issues about these complicated models work. The posterior predictive distribution (the distribution of data simulated from a model) has been used to flag modeldata discrepancies in the Bayesian literature, and several approaches have been developed. Posterior Predictive Sampling (PPS) where the usual available procedures are not applicable, therefore extending the work of Klein and Sinha [2, under the multivariate linear regression (MLR) model. The second problem considered is the calibration of posterior predictive pvalues so that they are uniformly distributed under some reference distribution for the data. Computation is difficult because the calibration process requires repeated approximation of the posterior for different data sets under the reference distribution. Phylodynamic model adequacy using posterior predictive simulations Sebastian Duchene. Department of Biochemistry and Molecular Biology, Bio21 Molecular Science and Biotechnology Institute, University of Melbourne, Australia This PDF is available to Subscribers Only. of the posterior predictive approach in two problems: estimation in a model with inequality constraints on the parameters, and estimation in a mixture model. In all Lynch, Western BAYESIAN POSTERIOR PREDICTIVE CHECKS 303 in which classical methods fail, but the Bayesian approach offers a feasible method for assessing model t. Simulating the posterior predictive distribution This is easy to do, assuming that you can simulate from the posterior distribution of the parameter, which is usually feasible. The sampling distribution of different posterior predictive pvalues (ppp's) in the case of J 4 dichotomous variables, N 100 observations (upper panels) and N 1000 (lower panels), and a true. A proposed diagnostic measure is the posterior predictive pvalue, an extreme value of which (i. , a value close to 0 or 1) suggests a misfit between the model and the data. The aim of this study was to evaluate the performance of the posterior predictive p value as an imputation diagnostic. A posterior predictive distribution is the conditional distribution of potential results, given the realized results, which could be obtained in contemplated replications of. Using the default posterior median point estimate, the indirect e ect estimate is 0: 016, that is, slightly lower than the ML value with a slightly higher posterior distribution standard deviation of 0: 013. In Bayesian statistics, the posterior probability of a random event or an uncertain proposition [clarification needed is the conditional probability that is assigned [clarification needed after the relevant evidence or background is taken into account. 111 Printed in Great Britain Model choice: A minimum posterior predictive loss approach BY ALAN E. GELFAND Department of Statistics, University of Connecticut, Storrs, Connecticut, U. (b) Find the prior predictive pdf for how late Romeo will be on the rst date and the posterior predictive pdf of how late hell be on the second date (if he gets one! Prior Predictive Distribution Before we observe the data, what do we expect the Predictive Distributions p. SPF example Normal model from Last class: Posterior Predictive What is the predictive distribution of a new observaton Y. Posterior distributions are computable from predictive distributions cases, previous work has determined the form of the conditional or has identied underlying nite dimen Predictive Distributions We realize that the uncertainty about the exact mean and variance to plug into the predictive formula is unclear. If we are uncertain about these values, using Posterior predictive checks to quantify lackoffit in admixture models of latent population structure David Mimnoa, David M. Engelhardtc, 1 aDepartment of Information Science, Cornell University, Ithaca, NY; bDepartment of Statistics, Department of Computer Science, Columbia University, New York, NY; and cDepartment of Computer Science, Center for Statistics. predictive check might be Bayesian, and the quantitative posterior predictive check attempts to reject a model without recourse to an alternative model, is ambiguous and predictive check might be Bayesian, and the quantitative posterior predictive check attempts to reject a model without recourse to an alternative model, is ambiguous and The methods are cross validation, a full posterior predictive assessment and two mixed predictive methods based on the approach proposed by Marshall and Spiegelhalter. An extension to the concept of the mixed prediction is described that is generalisable to three level hierarchical models. ) category StatisticsBayesian stat. Farrow School of Mathematics and Statistics Newcastle University Semester 2, our beliefs before we have seen data and the posterior predictive distribution describes our beliefs (119; 1220) with pdf f(1) ( ) 118! What is the posterior probability now of observing jvehicles. CPO evaluates the posterior predictive probability density but does not simulate from it, and thus lacks GGs ability to measure posterior predictive variance. On the other hand, GG lacks the cross validation that CPO provides (each site is evaluated using a model parameterized from all other sites). Posterior Mapping and Posterior Predictive Distributions 3 parsimony, and provides a statistically valid framework for accommodating uncertainty in the phylogeny and model parameters. Bayesian Inference, Posterior Predictive Distribution, MCMC, Happiness 1. Introduction Bayesian networks emerged about three decades ago as alternatives to conventional systemsoriented decision making and forecasting under uncertainty in probabilistic. posterior predictive distributions is conducted by sampling from each of these distributions, inferring summary statistics from the samples and generating a In this paper, we extend the implementation of Peterson's (2004) posterior predictive ap proach to binary responses. Although we limit our approach to the binary case, it can, however, be easily. The hierarchical model you describe is a generative model. The model you constructed can be used to generate fake data. This is a little different conceptually than using your model to make predictions. take the form of prior and particularly posterior predictive analysis and provides illustrations; and three, it provides a justi cation for the use of these tools in the DSGE context in defense against the standard criticisms for the use of these A. GelmanUnderstanding posterior predictive pvalues 4 time when the pvalue is 0. 4, that it happens 30 of the time when the pvalue is 0. the posterior predictive weights. (4) is simply the marginal likelihood p. the probability of observing data ygiven xm, averaging over any model parameter uncertainties. The term amand its deviation from apin the observation model can be considered as penalising bias be Additional resources for Posterior and Predictive Densities for Simultaneous Equation Models Sample text Bivariate numerical integration of 8, and 82, (, ) Four dimensional numerical integration is quite feasible at the present stage of technology..
-
Related Images: